Generative Art with Context Free Grammars

art python

Table of Contents

The Chomsky hierarchy defines four levels of formal grammars:

  1. Unrestricted (most powerful)
  2. Context Sensitive
  3. Context Free
  4. Regular (simplest)

Usually, the problem is checking whether a word belongs to a grammar.

Here, we only care about generating random expansions of a grammar. For this CFGs are a good choice because random expansion is easy to implement and they are not as limited as regular grammars.

If you're not familiar with the concept of context free grammars, read Context Free Grammars first.

Terminals of a grammar don't have to be characters, they can be (interpreted as) anything at all, for example functions that draw geometric shapes.

Turtle Grammars

One easy way to visualize the output of the expansion of a grammar is to interpret it as instructions for a Turtle Graphics program.

For the following examples, I'm using only three commands:

  1. move forward
  2. turn left / right
  3. scale (reduce the size of each forward step)

The expansions of grammars can be infinitely long, so we need a mechanism to prevent this from happening. I'm simply limiting the depth of the expansion to some value, after that all non-terminals are ignored.

Iteration

Let's start with a simple turtle rule system, to see how iteration can be implemented: 

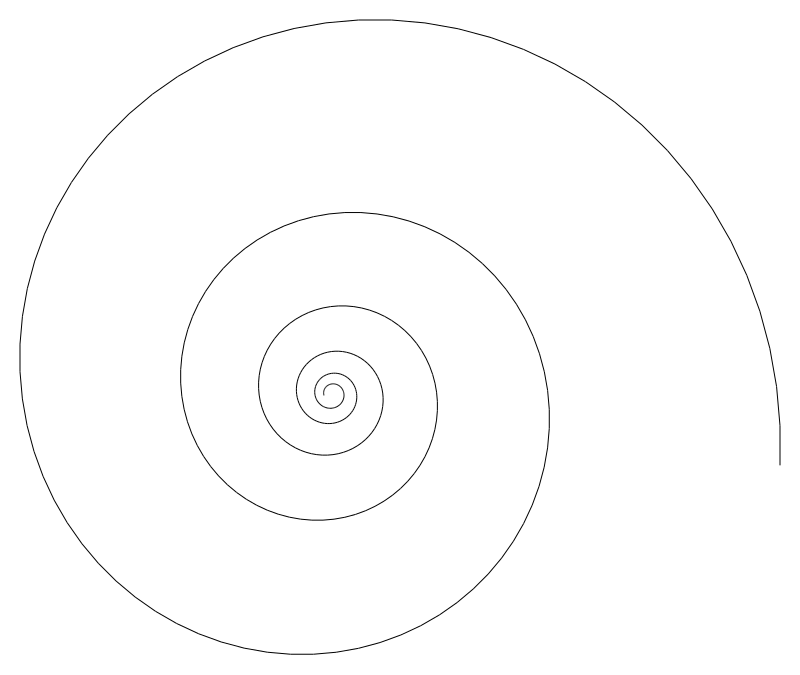
grammar.add_non_terminal('S', [
    lambda turtle: turtle.forward(),
    lambda turtle: turtle.turn_right(5),
    lambda turtle: turtle.scale_by(0.99),
    'S'
])

grammar.expand('S', turtle, 300)

For the examples, I'll be using a small python framework I've created instead of mathematical notation. If you want to follow along, download the code from https://github.com/l3kn/generative_cfg .

The main element of this framework is a Grammar . Non-terminals are just lists of either strings to reference another non-terminal or (anonymous) functions as terminals.

These terminal functions can act on some kind of state, in this case a turtle graphics object turtle .

Using grammar.add_non_terminal(name, body) new non-terminals can be added to the grammar.

A grammar can be expanded using the method grammar.expand(start_symbol, state, depth) .

Now it should be clear how the code above produces the image below, the non-terminal generative_art_with_cfgs_5f018c42d1e646f306da9aa4d3fa761e2205b12e.svg makes the turtle move forward, turns it to the right by 5 degrees, and then reduces its scale by a factor of generative_art_with_cfgs_dd12556d4a33f6abf8772143c0d2466bb94cfd74.svg .

Then the grammar is expanded to a depth of 300 using generative_art_with_cfgs_5f018c42d1e646f306da9aa4d3fa761e2205b12e.svg as start symbol.

spiral.png

Changing the rotation angle from 5 to 89.5 degrees leads to a very different result

spiral2.png

Branching 1 

from generative_cfg import *

backend = SVGBackend()
turtle = Turtle(backend)
grammar = Grammar()
scale = 0.6

grammar.add_non_terminal('Tree', [
    lambda t: t.store(),
    lambda t: t.turn_right(45),
    lambda t: t.forward(),
    lambda t: t.scale(scale),
    'Tree',
    lambda t: t.restore(),
    lambda t: t.turn_left(45),
    lambda t: t.forward(),
    lambda t: t.scale(scale),
    'Tree',
])

grammar.expand('Tree', turtle, 10)
backend.write('out.svg')

"Tree" draws a left “branch” and then another smaller "Tree", restores the turtles state and then draws a right “branch” and a second smaller "Tree".

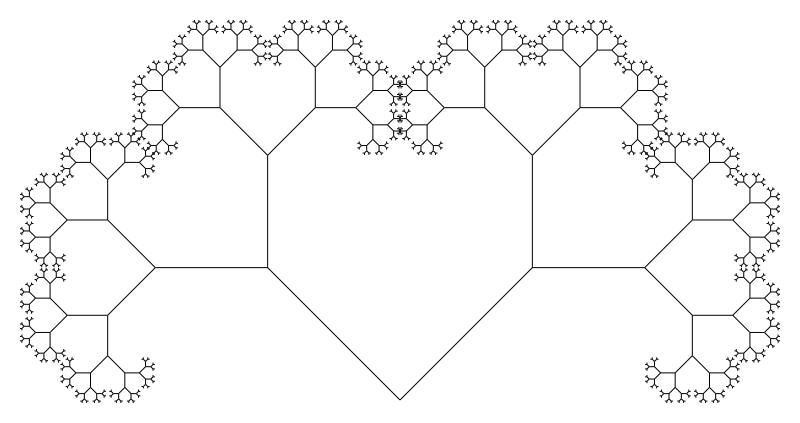
straight_tree.png

By adding two or more references to the rule into its RHS, we can generate all kinds of branching patterns.

Because we want the turtle to draw the left and right branches starting form the same position, we need a way to store and restore its state (instead of walking it back each time).

In the python framework, I've implemented this by pushing and popping the current position, direction and scale from a stack stored in the turtle object.

Branching 2

The tree above doesn't look very “natural”, real trees don't grow at straight angles.

By making a small step forward, then turning the turtle multiple times, we can draw smooth arcs.

Python's “array multiplications” ( [1,2] * 3 # => [1,2,1,2,1,2] ) can be used to save some work here. 

arc_right_segment = [
    lambda turtle: turtle.forward(0.1),
    lambda turtle: turtle.turn_right(5)
]
arc_left_segment = [
    lambda turtle: turtle.forward(0.1),
    lambda turtle: turtle.turn_left(5)
]

grammar.add_non_terminal('Arc Left', arc_left_segment * 10)
grammar.add_non_terminal('Arc Right', arc_right_segment * 10)

scale = 0.6
grammar.add_non_terminal('Tree', [
    lambda turtle: turtle.store(),
    'Arc Left',
    lambda turtle: turtle.scale_by(scale),
    'Tree',
    lambda turtle: turtle.restore(),
    'Arc Right',
    lambda turtle: turtle.scale_by(scale),
    'Tree',
])

grammar.expand('Tree', turtle, 10)

There is no need to wrap the second part in turtle.store() and turtle.restore() because we don't care where the turtle ends up after expanding the last part. (This is similar to tail-call-optimization for recursive functions).

tree.png

Randomness

In the introduction, we saw that grammars can have multiple non-terminals with the same name. We can use this to introduce an element of randomness into the generated images. 

grammar.add_non_terminal('Arc Left', arc_left_segment * 7)
grammar.add_non_terminal('Arc Left', arc_left_segment * 10)
grammar.add_non_terminal('Arc Left', arc_left_segment * 13)
grammar.add_non_terminal('Arc Right', arc_right_segment * 7)
grammar.add_non_terminal('Arc Right', arc_right_segment * 10)
grammar.add_non_terminal('Arc Right', arc_right_segment * 13)

By randomly using shorter or longer arcs, a different tree is generated each time the script is run.

tree2_1.png tree2_2.png tree2_3.png

Evolving Rule Sets

Time to explore a different direction from the same starting point, to see how complex grammars can be built with small steps.

Starting Point

Make the branches straight at an 60deg angle, and grow three "trees" starting from a root in the center. 

grammar.add_non_terminal('Branch Right', [
    lambda turtle: turtle.forward(1.0),
    lambda turtle: turtle.turn_right(60)
])
grammar.add_non_terminal('Branch Left', [
    lambda turtle: turtle.forward(1.0),
    lambda turtle: turtle.turn_left(60)
])

grammar.add_non_terminal('Root', [
    'Tree',
    lambda turtle: turtle.turn_left(120),
    'Tree',
    lambda turtle: turtle.turn_left(120),
    'Tree',
])

scale = 0.5
grammar.add_non_terminal('Tree', [
    lambda turtle: turtle.store(),
    'Branch Left',
    lambda turtle: turtle.scale(scale),
    'Tree',
    lambda turtle: turtle.restore(),
    # We can't TCO anymore
    lambda turtle: turtle.store(),
    'Branch Right',
    lambda turtle: turtle.scale(scale),
    'Tree',
    lambda turtle: turtle.restore(),
])
flower.svg

Randomly Terminating Branches

… by adding an empty "Tree" non-terminal 

grammar.add_non_terminal('Tree', [
    lambda turtle: turtle.store(),
    'Branch Left',
    lambda turtle: turtle.scale(scale),
    'Tree',
    lambda turtle: turtle.restore(),
    # We can't TCO anymore
    lambda turtle: turtle.store(),
    'Branch Right',
    lambda turtle: turtle.scale(scale),
    'Tree',
    lambda turtle: turtle.restore(),
], 8)
grammar.add_non_terminal('Tree', [])

flower1_00.svg flower1_01.svg

Randomized Scaling

Now extract a "Scale" non-terminal that scales the turtle only 50% of the time. 

scale = 0.5
grammar.add_non_terminal('Scale', [
    lambda turtle: turtle.scale(scale),
])
grammar.add_non_terminal('Scale', [])

flower2_00.svg flower2_01.svg flower2_02.svg flower2_03.svg

Thick Lines

Using a ThickTurtle , we can draw lines with different widths 

from generative_cfg import *

# ...

backend = SVGBackend()
turtle = ThickTurtle(backend)
turtle.thickness = 0.05

grammar.expand('Root', turtle, 12)

and modify scale to adjust the turtles scale, too. 

scale = 0.5
grammar.add_non_terminal('Scale', [
    lambda turtle: turtle.scale(scale),
    lambda turtle: turtle.scale_thickness(0.6),
])
grammar.add_non_terminal('Scale', [])

flower3_00.svg flower3_01.svg flower3_02.svg flower3_03.svg

Decoration

To make the result more visually interesting, we can add random "decoration" elements to the grammar. 

grammar.add_non_terminal('Circle', [
    lambda turtle: turtle.draw_filled_circle(0.2),
])
grammar.add_non_terminal('Circle', [
    lambda turtle: turtle.draw_circle(0.2),
], 2)
grammar.add_non_terminal('Circle', [], 8)

grammar.add_non_terminal('Tree', [
    lambda turtle: turtle.store(),
    'Branch Left',
    'Scale',
    'Circle',
    'Tree',
    lambda turtle: turtle.restore(),
    lambda turtle: turtle.store(),
    'Branch Right',
    'Scale',
    'Circle',
    'Tree',
    lambda turtle: turtle.restore(),
], 8)

flower4_00.svg flower4_01.svg flower4_02.svg flower4_03.svg flower4_04.svg

Further Work

There are a bunch of things that can be done to extend the ideas presented here.

A simple change would be to add a “finally” function to rules that is executed once the expansion depth has reached some limit. As far as I can tell, this would be equivalent to context-free L-Systems and can be used to draw all kinds of fractals and plants.

The turtle graphics implementation used here is very limited and it would be easy to extend it to support drawing circles, polygons or thick lines.

Another direction could be to implement different kinds of states (besides turtle graphics) that the grammar can operate on. (Hint: Quadtrees and Octrees are one possibility).

If you have any questions about how this works, how to implement it the programming language of your choice, or if you want to share an image you generated, feel free to contact me at cfg <at> leonrische.me

References

Turtle Graphics are a great way to teach programming to children, if you are interested in that angle, I recommend the book “Mindstorms: Children, Computers and Powerful Ideas” by Seymour Papert.

For some background on the LOGO language and its history, visit https://el.media.mit.edu/logo-foundation/what_is_logo/index.html

With a few small changes, the context free grammars described in this article can be expanded to context-free L-Systems which can be used to model the growth of different kinds of plants. The book “The Algorithmic Beauty of Plants” is a great introduction into this topic and can be downloaded for free at http://algorithmicbotany.org/papers/ .

Context Free Art is a program generates (colored) images from CFGs, the website contains a large collection of example programs / images.

Closing the circle, thanks to turtletoy user Jurgen an interactive implementation of the final ruleset can be found on turtletoy - Hexagonal Tree .

If you have an idea how this page could be improved or a comment send me a mail.