Table of Contents
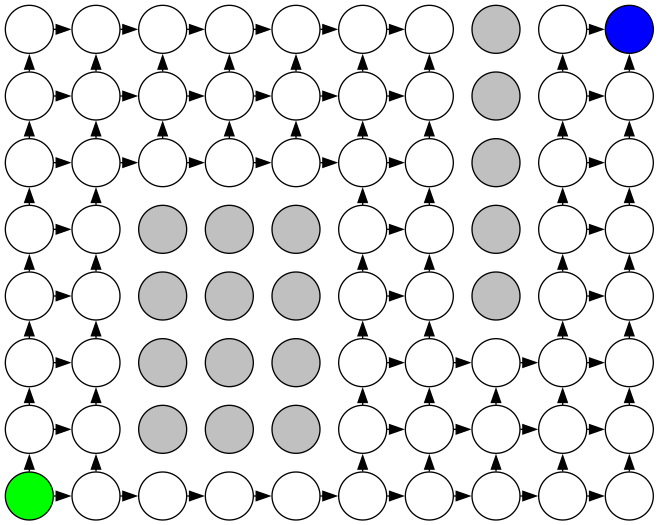
Imagine we're given a grid of size
, with rectangular obstacles
placed on it.
Starting from the bottom-left cell and only moving right or up onto cells not occupied by an obstacle, how many different paths are there to the top-right cell?
Representing the Grid
We will represent each cell of this grid as a nodes with properties to encode its positions:
UNWIND range(1, $width) AS x
UNWIND range(1, $height) AS y
CREATE (:Cell {x: x, y: y})

Cells blocked by an obstacle get an additional
Blocked
label.
We'll describe each obstacle by the ranges of X and Y coordinates it
covers:
UNWIND range($x0, $x1) AS x
UNWIND range($y0, $y1) AS y
MATCH (c {x: x, y: y})
SET c:Blocked

To model movement between nodes, we'll add relationships between each unblocked node and its unblocked neighbors to the right and above.
MATCH (c1:!Blocked), (c2:!Blocked) WHERE (c2.x = c1.x AND c2.y = c1.y + 1) OR (c2.y = c1.y AND c2.x = c1.x + 1) CREATE (c1)-[:HAS_PATH]->(c2)
Counting Paths
One way to count the paths is to query all possible paths from the source to the target node:
MATCH ({x: 1, y: 1})-[r:HAS_PATH*]->({x: $width, y: $height})
RETURN count(r) AS pathCount
This will be very slow for most large grids.
A faster method is to attach a new
pathCount
property to nodes
(initially
NULL
) and compute it step-by-step. We'll set it to
1
for the node we start at:
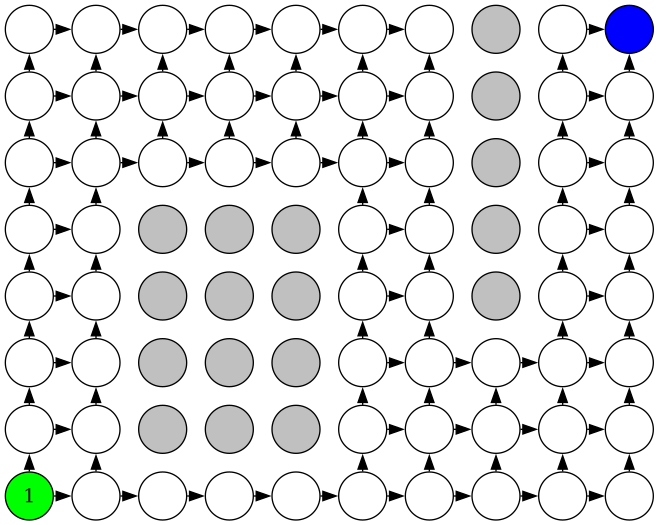
MATCH (c {x: 1, y: 1}) SET c.pathCount = 1
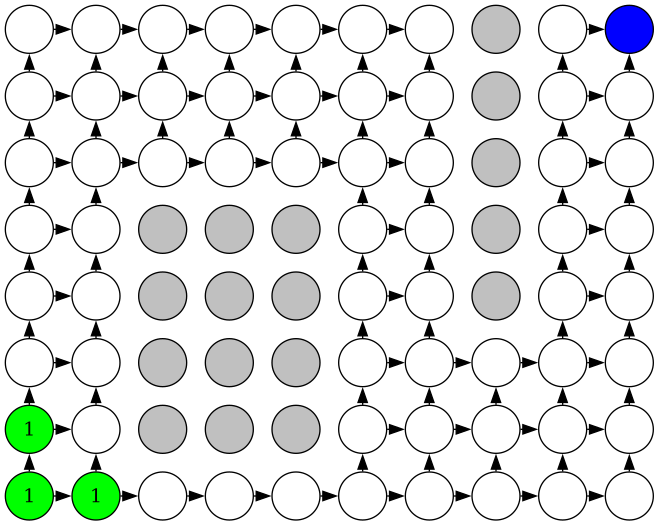
Each unblocked node can be reached either from the below or from the
left, so the
pathCount
of this node will be the sum of the path
counts these neighboring nodes, if those have already been computed:
MATCH (c1)-->(c2) WITH c2, collect(c1) AS incoming, sum(c1.pathCount) AS pathCount WHERE ALL(i IN incoming WHERE i.pathCount IS NOT NULL) SET c2.pathCount = pathCount
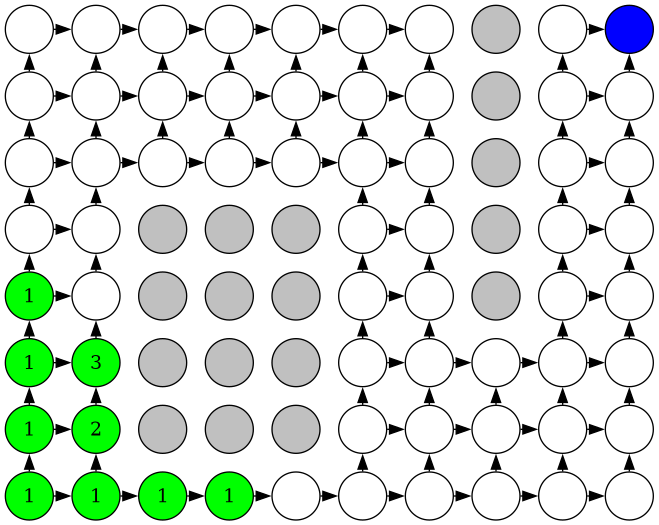
After running this query two more times, the graph looks like this:
Now we run into a problem: Cypher is a
declarative query language
and (to my understanding) doesn't natively support running a query in
a loop while accessing data written to the graph in the previous
iteration. More precisely,
UNWIND
and similar constructs run in a
single database transaction.
One way to work around this is to use apoc.cypher.doIt from the apoc library:
UNWIND range(1, $steps) AS i
CALL apoc.cypher.doIt(
"
MATCH (c1)-->(c2)
WITH c2, collect(c1) AS incoming, sum(c1.pathCount) AS pathCount
WHERE ALL(i IN incoming WHERE i.pathCount IS NOT NULL)
SET c2.pathCount = pathCount
",
{}
) YIELD value
This will
YIELD
and
RETURN
some intermediate values, which we can ignore.
Note: the path counts of each node will not be shown in the remaining images to avoid layout issues.
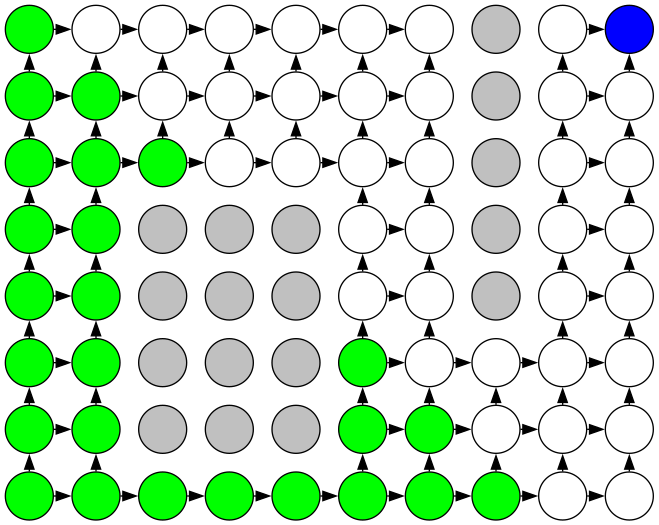
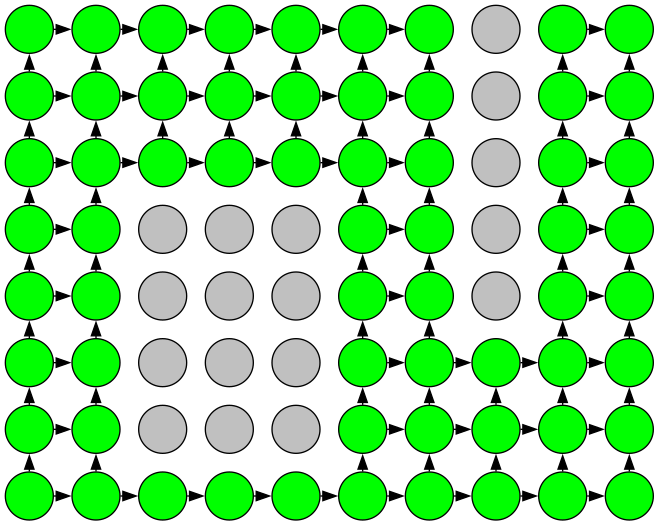
After repeating the query
steps = width + height - 2
times, the
result can be read out from the
pathCount
property of the target
node. Proving why this is true is left as an exercise for the reader.
This approach should generalize to all acyclic graphs and can be extended to perform different kinds of computation on the nodes.